Chuckie's Blog

算法总结c++版本

发表于 更新于 分类于
本文字数： 27k 阅读时长 ≈ 24 分钟

hot 100

  • 1 两数之和

    • 时间复杂度O（n）,空间O（n）
    • 哈希map, find, count(时间复杂度都为O(1), 最坏情况为O(n))

  • 2 两数相加 链表

    • 初始化pre,每次相加包括pre, 整除10更新pre

  • 3 无重复字符的最长子串

    • 滑动窗口+hashset

  • 4 寻找两个正序数组的中位数

    • 二分查找，边界，各种情况分析，易错，复习

  • 5 最长回文子串

    • 从中心往两边扩展，分为偶数和奇数情况

  • 10 正则表达式匹配

    • 动态规划

  • 11 盛最多水的容器

    • 双指针，策略：矮的往前走可能变大，高的往前走，由于高度还是矮的决定所以只能变小，所以最终，每次选择矮的一侧往前走，并更新面积

  • 15 三数之和

    • 排序+双指针， 三层循环的内两层可以改为相向逼近的双指针
    • 注意内层元素大于等于外层，但内外层可以可以元素相同，同层不能元素相同，还有双指针相遇时可以提前结束循环，细节很多，易错，复习

  • 17 电话号码的字母组合

    • 回溯，递归

  • 19 删除链表的倒数第 N 个结点

    • 官方要求一次遍历，但官方解答却是快慢指针，仍然是两次遍历
    • 直接遍历一次，并用数组存下每个节点指针，最有用数组直接O(1)就可以索引到倒数n+1个节点，实现删除了

  • 20 有效的括号

    • 栈，奇数个直接return false

  • 21 合并两个有序链表

    • 归并，注意定义一个空的节点pre，便于编程

  • 22 括号生成

    • 回溯，需要强化思路，复习

  • 23 并K个升序链表

    • 优先队列

  • 31 下一个排列

  • 32 最长有效括号

  • 33 搜索旋转排序数组

    • 看官方二分搜索的写法，更加清晰
    • 每次二分，总有一部分是有序的，若target在有序中，则正常二分，若不在，则是一个子问题，继续二分

  • 34 在排序数组中查找元素的第一个和最后一个位置

    • 学习如何二分查找找到第一个大于等于target的位置，第一个大于target的位置

  • 39 组合总和

    • 回溯

  • 42 接雨水

    • 不会，看解析，先理解动态规划，再理解双指针
    • 复习复习复习

  • 46 全排列

    • 回溯，swap方式动态维护数组，递归到底，维护的数组就是最终结果，直接加入res即可，不用额外维护一个排序结果的数组

  • 48 旋转图像

  • 49 字母异位词分组

    • 字母排序+ hashmap

  • 53 最大子数组和

    • 动态规划: f[i] = max(nums[i], f[i-1]) // 如果此时取了nums[i]则表示前面的舍弃，新的区间从i开始

  • 55 跳跃游戏

    • 贪心，看代码更易理解

  • 56 合并区间

  • 62 不同路径

    • 坐标型动态规划

  • 64 最小路径和

    • 坐标型动态规划

  • 70 爬楼梯

    • 动态规划

  • 72 编辑距离

    • 动态规划

  • 75 颜色分类

    • 三路快排思想

  • 76 最小覆盖子串

    • 滑动窗口 + hashmap记录字符满足个数，并记录

  • 78 子集

    • 回溯

  • 79 单词搜索

    • 递归回溯，开标记数组

  • 84 柱状图中最大的矩形

    • 单调栈，第一次学习，复习

  • 85 最大矩形

    • 84升级版，复习

  • 94 二叉树的中序遍历

    • 递归和非递归，栈

  • 96 不同的二叉搜索树

    • 动态规划，不太懂，复习

  • 98 验证二叉搜索树

    • 注意利用性质
      • 二叉搜索树中序遍历正好是升序
      • 递归，自顶向下，传递左子树和右子树的范围

  • 101 对称二叉树

    • 递归和迭代写法都不是很熟悉，需要复习复习

  • 102 二叉树的层序遍历

    • 用队列长度记录每层的元素个数，从而分层

  • 104 二叉树的最大深度

    • dfs,bfs

  • 105 从前序与中序遍历序列构造二叉树 待写

    • 递归构建，有难度，不熟悉，复习
      • 先序遍历的第一个元素就是中序遍历的中间位置，定位到中序遍历的中间位置，则可以将左右分为左子树和右子树，而左子树确定后可以确定长度，又可以反过来让先序遍历的数组明确左子树和右子树的区间，然后进行递归划分
    • 非递归写法待学习

  • 114 二叉树展开为链表 待写

    • 先前序遍历搜集顺序到数组中，再通过数组顺序构建链表
    • 先序遍历过程中展开为链表，利用栈

  • 121 买卖股票的最佳时机

    • 记录左边最小值，遍历一次

  • 124 二叉树中的最大路径和

    • 递归,官方解答思路更清晰

  • 128 最长连续序列 待写

    • 哈希

  • 136 只出现一次的数字 待写

    • 异或运算，性质，，，学习，记忆，异或运算符号

  • 139 单词拆分

    • 动态规划

  • 141 环形链表

    • 快慢指针

  • 142 环形链表 II

    • 141升级，巧妙，记忆

  • 146 LRU 缓存

    • 直接用list，stl的list就是双向指针
1
2
mp.erase(ls.back().first); // 先mp移除，因为先ls，这里还要使用ls
ls.pop_back();

hot 100（add）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
  bool isMatch(string s, string p) {
    // f[i][j] 记录s前i个元素是否可以被p的前j个元素匹配  记录bool
    // f[i][j] = f[i-1][j-1]  s[i-1] == p[j-1] || p[j-1] == '.'
    //         = f[i-1][j]    p[j-1] == '*' && (p[j-2] == s[i-1] || p[j-2] == '.')
    //         = f[i][j-2]    p[j-1] == '*'  // 因为".*" "s[i-1]*"可以匹配0个，即可以不用
    // 初始化
    // f[0][0] = true;
    // f[0][1---m] = f[0][j-2] && p[j-1] == '*' // 可以匹配0个
    // f[1---n][0] = false;

    int n = s.size();
    int m = p.size();
    vector<vector<bool>> f(n+1, vector<bool>(m+1, false));
    f[0][0] = true;
    for(int i = 1; i <= n; ++i){
      f[i][0] = false;
    }
    for(int j = 1; j <= m; ++j){
      if(p[j-1] == '*'){
        f[0][j] = f[0][j-2];
      }else{
        f[0][j] = false;
      }
    }

    for(int i = 1; i <= n; ++i){
      for(int j = 1; j <= m; ++j){
        if(p[j-1] == '*'){
          f[i][j] = f[i][j-2];
          if(p[j-2] == s[i-1] || p[j-2] == '.'){
            f[i][j] = f[i][j] || f[i-1][j];
          }
        }else{
          f[i][j] = f[i-1][j-1] && (s[i-1] == p[j-1] || p[j-1] == '.');
        }
      }
    }
    return f[n][m];
  }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
public:
  int minDistance(string w1, string w2) {
    int n = w1.size();
    int m = w2.size();
    // f[i][j] 记录w1的前i个元素变为w2的前j个元素的最少操作次数
    // f[i][j] =  min(f[i-1][j-1] 相等 ,f[i-1][j] +1 删除, f[i-1][j-1]+1 替换, f[i][j-1]+1 插入) 
    // 初始化
    // f[0][0,,j,,m] = j  插入
    // f[0,,i,,n][0] = i  删除
    vector<vector<int>> f(n+1, vector<int>(m+1));
    // 放在外面单独处理性能更好
    for(int i = 0; i <=n; ++i){
        f[i][0] = i;
    }
    for(int j = 0; j <=m; ++j){
        f[0][j] = j;
    }
    for(int i = 1; i <= n; ++i){
      for(int j = 1 ; j <= m; ++j){
        // if(i == 0){
        //   f[i][j] = j;
        //   continue;
        // }
        // if(j == 0){
        //   f[i][j] = i;
        //   continue;
        // }
        // 用临时变量记录比每次使用f[i][j]性能更好
        int left = f[i-1][j] + 1;
        int right = f[i][j-1] + 1;
        int lr = f[i-1][j-1] + 1;
        if(w1[i-1] == w2[j-1]) lr -= 1;
        f[i][j] = min(lr, min(left, right));
        // f[i][j] = f[i-1][j] + 1;
        // f[i][j] = min(f[i][j], f[i-1][j-1]+1);
        // f[i][j] = min(f[i][j], f[i][j-1]+1);

        // if(w1[i-1] == w2[j-1]){
        //   f[i][j] = min(f[i][j], f[i-1][j-1]);
        // }
      }
    }
    return f[n][m];
  }
};

剑指offer(专项突破)

1
2
3
4
5
6
7
8
输入范围[−2^31, 2^31−1]
考虑边界情况，可能溢出的情况
1 a = -2^31  b = -1   res = 2^31 溢出  return 2^31-1
2 a = -2^31  b = 1  res = -2^31
3 b = -2^31  a = -2^31 res = 1
4 b = -2^31  a = any  res = 0
5 a,b符号都调整为负后  if(a > b) return 0
  a = -2^31 调为正则会溢出  所以都统一调为负
1
2
3
4
5
6
7
8
9
10
11
12
// masks[i]记录第i个单词的位掩码  
// int 型有32个比特位
// 26个英文字母就26个比特位就可以表示
// 所以 vector<int> masks, masks[i]就可以记录一个单词的位掩码

// a  1
// b  10
// c  100
// abc 111
// af  100001

// c  所在的位  1 << 'c' - 'a'    1 左移 2位  即 100

每日一题

1
2
3
4
5
6
7
// resid = 1 mod k
// nnew = nold * 10 + 1
// residnew = nnew mod k = (nold * 10 + 1) mod k = ((nold%k) * 10 + 1)%k
//          = (residold * 10 + 1)%k
// resid = (resid * 10 + 1)%k
// resid == 0 表示可以被整除
// resid 重复出现则表示进入循环 ********重要：退出判断*******
  • 2611 老鼠和奶酪
    • 贪心+排序/优先队列
    • 注意问题的转化，将问题转化为在n个数中选择k个数，使得和最大，也就是求n个中前k个大的数的和 巧妙！！！

题型

数组

排序应用

对撞指针

滑动窗口

定宽窗口和变宽窗口有区别

查找

set

map

1
2
3
4
5
x,y都是整数
x: [-2*10^4, 2*10^4]  y: [0, 2*10^4] x+y后区间是连续的所以会重复
x = x * (2*10^4+1)后  x的间距变为2*10^4+1 正好可以容下y的区间  x+y就不会重复， 每个x加上y后区间都不和其它x加上y的区间重合

-40002， -20001， 0 ， 20001， 40002 +y--->[-60002,-40002] [-40001, -20001] [0, 20000] [20001,40001] [40002, 60002] q

查找表+滑动窗口

二分搜索树+滑动窗口

lower_bound 返回指向首个不小于给定键的元素的迭代器 (公开成员函数)
upper_bound 返回指向首个大于给定键的元素的迭代器

差分数组

注意对交点(增加和减少的汇聚点)的处理，根据业务情况确定在哪减

数学

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 快速幂
int ksm(int a, int b) { // 计算a^b
  int ans = 1;
  int base = a;
  while (b) {
    if ((b&1) != 0) {
      // 避免ans越界 可以用上线除以base 看是否小于ans  如果是则可以*base  否则不能
      ans *= base;
    }
    base *= base;
    b >>= 1;
  }
  return ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
// 快速乘
int ksc(int a, int b) { // 计算a*b
  int ans = 0;
  int base = a;
  while (b) {
    if ((b&1) != 0) {
      ans += base;
    }
    base += base;
    b >>= 1;
  }
  return ans;
}

快速幂/快速乘： 下面的面试部分有讲解

最大公因数： gcd(n,m)

辗转相除法

1
2
3
4
// 辗转相除法
int gcd(int n, int m){
    return n%m == 0 ? m : gcd(m, n%m);
}

最小公倍数: clm(n,m)

1
2
3
4
5
6
7
8
a = n/gcd(n,m);
b = m/gcd(n,m);

clm(n,m) = a * b * gcd(n,m) = n*m/gcd(n,m)
    
int clm(int n, int m){
    return n*m/gcd(n,m);
}
  • offer专项 071 按权重生成随机数
    • 就是在权重范围内生成随机数，随机数落在哪个区间，就返回那个区间对应的数

字符串

对字符串排序

两个字符串是否相等，直接用s == t判断， 比自己比较快

线段树

视频讲解

  • LCR 058. 我的日程安排表 I

    • map + 二分查找，简洁，易懂

      • 容器查找为空则结果等于begin，容器为空的情况下begin == end 不熟悉，复习

    • 线段树

      • lazy记录这个区间所有点都已预定 tree记录这个区间有至少一个点被预定过了

二进制

异或性质

  • a^b = b^a
  • x = a^b —-> a = x^b
  • offer专项 067 最大的异或
    • 字典树处理，看解析，第一个评论解析比官方更易理解
    • 复习 容易忘

二分查找

offer专项 068 — 073

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long long)mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
};

栈、队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<string> split(const string& s, char k) {
    vector<string> res;
    string cur;
    for (auto& c : s) {
        if (c == k) {
            if (cur != "") res.push_back(cur);
            cur.clear();
        } else {
            cur += c;
        }
    }
    if (cur != "") res.push_back(cur);
    return res;
}

递归

队列

BFS最短路径

  • 279 完全平方数
    • 因为是需要最少的平方数，所以就是最短路径，所以BFS效果好
      • BFS倒着入队效果可能更好(最大的平方数先入队，例如对于15，第一层入队顺序：6(15-9)， 11(15-4)，14(15-1))
    • 数学方法效果最好 记忆结论
    • 动态规划 待学习， 已学习，效果不如BFS，因为对于全是1的情况的都考虑了，换成递归的形式深度会很大，所以效果不如BFS
    • BFS 去重的理解（对于相同值，前面入队过的值至少深度是小于等于当前值的，所以当前值继续只会大于等于前面的值，所以可以不入队）
  • 127单词接龙
    • 巧妙构建树
    • 双向BFS的思想
  • 126 单词接龙 II
    • 回溯 待学习

优先队列

链表

1 快慢指针定位链表中点时，前面添加dummy，这样定位就正好在中间了

-1 0 1 2 3 4 5 n = 6 中间位置：2

-1 0 1 2 3 4 5 6 n = 7 中间位置：3

2 不方便while的就直接用for确定移动的次数，这样不容易出错

3 充分利用滑动的指针：148 自底向上的cur的使用，复习

常见记录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// 反转链表
ListNode* reverse(ListNode* head){
  ListNode* pre = nullptr;
  while (head)
  {
    ListNode* temp = head->next;
    head->next = pre;
    pre = head;
    head = temp;
  }
  return pre;
}

// 合并两个单链表 l1长于l2的情况可以完全链接上  l2长于l1时，l2后半段会丢失
void mergeList(ListNode* l1, ListNode* l2){
  ListNode* ll1;
  ListNode* ll2;
  while (l1 && l2)
  {
    ll1 = l1->next;
    ll2 = l2->next;
      
    l1->next = l2;
    l1 = ll1;
      
    l2->next = l1;
    l2 = ll2;
  }
}

// 找链表的中点
ListNode* midList(ListNode* head){
  ListNode* slow = head;
  ListNode* fast = head;
  while (fast->next && fast->next->next)
  {
    slow = slow->next;
    fast = fast->next->next;
  }
  return slow;
}

树

通过空节点判断递归到底，判断更简洁

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
        if(!root1 && !root2){
            return nullptr;
        }else if(!root1){
            return root2;
        }else if(!root2){
            return root1;
        }else{
            root1->val = root1->val + root2->val;
            root1->left = mergeTrees(root1->left, root2->left);
            root1->right = mergeTrees(root1->right, root2->right);
            return root1;
        }

// 上面可简写为下面
 		if(!root1) return root2;
        if(!root2) return root1;
		// 上面两行包括了都为空的情况
        root1->val = root1->val + root2->val;
        root1->left = mergeTrees(root1->left, root2->left);
        root1->right = mergeTrees(root1->right, root2->right);
        return root1;

单调栈

栈存储索引，通过索引取值，就不用存键值对，空间开销更小

在一维数组中对每一个数找到第一个比自己小/大的元素。这类“在一维数组中找第一个满足某种条件的数”的场景就是典型的单调栈应用场景

  • 找到右边第一个比自己小的值
    • 往右走
      • cur比栈顶大则入栈
      • cur比栈顶小则while(cur比栈顶小)出栈，直到比栈顶大则继续入栈
        • 出栈元素右边第一个比自己小的元素就是cur, 进行记录
        • 技巧： cur左边第一个比自己大元素就是cur可以入栈时，栈顶的元素 （典型案例：84）

典型案例：84

  • 739 每日温度

    • 栈存储index值，通过 t[st[i]]拿到值

  • 84 柱状图中最大的矩形

    • 找到左边第一个比当前元素小的，找到右边第一个比当前元素小的
    • 注意初始化

  • 85 最大矩形

    • 需要依赖84才能做出来，没有84的基础基本做不了

  • 581 最短无序连续子数组

    • 感觉和单调栈没啥关系
    • 双指针，模拟正常思考过程
    • 往右走，则需要一直递增，若不满足则记录该位置，该位置是需要往左移动的，往右走完，记录的就是最右需要往左移的位置
      • 往左走，则需要一直低价，若满足，，，

  • 42 接雨水

    • 动态规划易理解 推荐
    • 双指针的策略没有理解透彻，复习，对动态规划的优化，不易理解
    • 单调栈不简洁，不易理解

回溯

1 先排序有利于解决问题 有重复元素则排序

2 对于重复的元素，采用标记的方式，相同的元素只有在前面的元素使用后后面的元素才能使用，保证排列组合不会重复

3 尽可能在原数组上标记，不用额外开空间，节省了空间，性能也更好

  • 17 电话号码的字母组合
  • 22 括号生成
    • 不熟练，复习，，，，
    • 每次有两个选择，要么加入’(‘、要么加入’)’, 所以需要回溯保证，每层只加入一种
  • 93 复原 IP 地址 重复做，考察细节
  • 131分割回文串
    • 回溯+动态规划 提前预处理所有可能的回文串 因为回溯过程中有重复计算
    • 动态规划记录所有回文串 再学习
      • 从对角线开始往两边扩展
      • 初始化顺序，根据下一步要是的情况，决定这一步先初始化哪里
1
2
3
4
5
6
7
8
9
10
11
12
// 动态规划记录所有回文串
// f[i][j] = f[i+1][j-1] && s[i]==s[j]
// f[i][j] = true && i >= j
// "aa" f[0][0] = true, f[1][0]==true 
// f[0][1] == f[1][0] && s[0]==s[1]   只有f[1][0]==true 才能保证结果正确

f.assign(n, vector<bool>(n,true));
for(int i = n-1; i >=0; --i){ // 注意i是从大到小开始初始化，因为递推公式需要用f[i+1][j-1]所以需要先知道i+1
  for(int j = i+1; j<n; ++j){
    f[i][j] = (s[i] == s[j]) && f[i+1][j-1];
  }
}

排列组合

先排序有利于解决问题

对于重复的元素，采用标记的方式，相同的元素只有在前面的元素使用后后面的元素才能使用，保证排列组合不会重复

全排列

  • 46 全排列

    • 动态维护数组的方式 巧妙 学习

  • 47 全排列 II

    • 注意去重的方法 复习
    • 有重复元素且每个元素只能使用一次
      • 解决方案： 排序，标记使用过的，相同的元素，只有前面一个使用过了后面的才能使用

组合

二维平面的回溯

使用偏移量数组简化代码量，但可能影响性能，多了判断

  • 79 单词搜索
    • 在原数组上进行标记，不用额外开空间，节省了空间

floodfill

n皇后问题

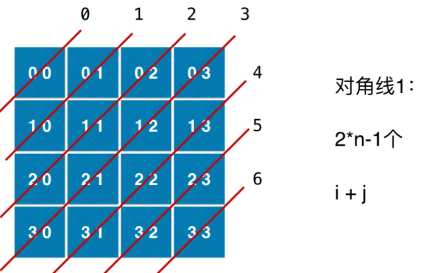
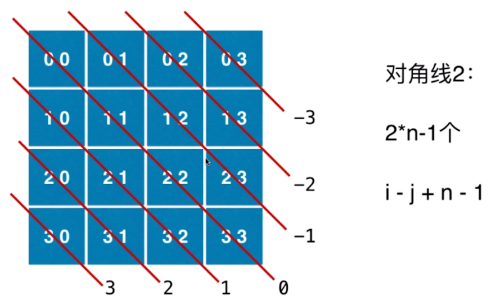
  • 51 N 皇后
    • 看解析 看视频讲解8-8 待复习
    • 下图的方式标记斜线是否可以放置，也可以用二进制数来标记(巧妙)
      • 二进制部分没懂 待学习
  • 52 N皇后2

image-20221117203645300

image-20221117203736258

  • 37 解数独
    • 参考官方解答，对于3*3块的记录
    • 位运算优化待学习

  • 301 删除无效的括号

    • 困难，待做
    • 广度优先，最短，最少就用广度优先
    • 不会不会不会

  • 494 目标和

  • offer专项081- 087

    • 有重复元素则排序，并保证和前一个元素不同，如果和前一个元素相同则continue
    • 无重复元素全排列可以用swap
    • 有重复元素全排需要使用标记，不能用swap, 因为swap后会乱序，导致不能判断和前一个元素是否相同
    • 排序
      • 保证和前一个元素不同
      • 标记

  • offer专项085. 生成匹配的括号

    • 不熟悉，复习

广度深度优先

在递归开始或者在进入递归前进行标记，这样不容易出错

构建图：

  • 字符串等情况，先将字符串映射为数字，便于使用vector存储图结构

广度优先：一般用于计算最短路径的场景题

  • 105. 从前序与中序遍历序列构造二叉树

  • 106 二分图

    • 不熟悉，复习
    • 用序号来标记两个分组

  • 107 矩阵中的距离

    • 动态规划和广度优先 复习 不熟悉
    • 动态规划
      • 从某个0到某个1的距离计算，先向下再向右和先向右再向下是等价的
    • 广度优先
      • 关键点是每次只扩展一步，且对已经扩展的进行标记

  • 108 单词演变

    • 不会， 复习
    • 图的构建不熟悉，复习
    • 遍历记得标记已经遍历的元素
    • 广度优先，找最短路径，记录层数的方法

  • 111 计算除法

    • 构建图，不熟悉，复习
    • 广度优先，记录路径

动态规划

https://chuckiewill.github.io/2022/01/26/C++/c++algo/

offer专项 088-105

贪心

  • 455. 分发饼干
  • 392. 判断子序列
  • 435. 无重叠区间
    • 类似 动态规划中求最长递增子序列 300 (O(n^2))
    • 此题用动态规划 不通过 运行时间过长
    • 贪心思路 （O(n)）
      • 注意:每次选择中，每个区间的结尾很重要
      • 结尾越小，留给了后面越大的空间，
      • 后面越有可能容纳更多区间
      • 按照区间的结尾排序，
      • 每次选择结尾最早的，且和前一个区间不重叠的区间
1
2
// 按照区间的结尾排序，
// 每次选择结尾最早的，且和前一个区间不重叠的区间

牛客面经

有环或无环链表的相交问题

情况2：一个链表有环，一个链表无环，这种情况不可能相交 相交后共用 一个有环 另一个一定也有 可以相交在环之前 也可以相交在换上

两个链表相交，且两个链表的入环节点是同一个（loop1 = loop2，就认为 loop1 和 loop2 是终止节点，问题就变成了两个无环链表找第一个相交节点） loop1 = loop2表示入环点相同 就可以确定是情况2了，，，

重要思想：如果两个单链表有共同的节点，那么从第一个共同节点开始，后面的节点都会重叠，直到链表结束。
因为两个链表中有一个共同节点，则这个节点里的指针域指向的下一个节点地址一样，所以下一个节点也会相交，依次类推

  1. 怎么判断链表相交
  2. 怎么判断链表有环
  3. 怎么找到环入口地址？为什么这么找？怎么证明
  4. 怎么判断两个有环链表是否相交？

求链表的中间结点

在二叉树中找路径最长的两个点

  • dfs, 并维护一个长度为2的队列，每次递归到底，深度更深则将该点加入队首，并判断队列长度是否大于2，若大于则删除队尾

拼多多 3.12

多多君最近在研疗一种编码期法、对于连境出机的字花，用变的长提来改元，发提这样可以有

PS

前缀和+哈希表

位掩码，字符串求交

双指针，有序

滑动窗口，用左右索引记录范围(offer 017 专项)

快慢指针

  • 快慢指针定位链表中点时，前面添加dummy，这样定位就正好在中间了

性能

  • 注意可以传引用的尽量传引用，字符串传值和传引用性能差距10倍
  • unordered_map中不使用的元素实时移除，性能更高
  • 多级索引查询，用临时变量存储， 性能快一倍
1
2
3
4
5
6
7
8
9
10
11
12
for(int i = 1; i <=n; ++i){
    for(int j = target; j >= nums[i-1]; --j){
        f[j] = f[j] || f[j-nums[i-1]];
    }
}

for(int i = 1; i <=n; ++i){
    int a = nums[i-1]; // 临时变量存储
    for(int j = target; j >= a; --j){
        f[j] = f[j] || f[j-a];
    }
}
  • 移除字符串中一个元素 code: 1048
    • 用substr拼接比erase快一倍，内存消耗也更小，内存消耗大，可能是函数调用
1
2
3
4
5
6
7
8
9
10
11
12
// substr拼接
for (int i = 0; i < word.size(); i++) {
    string prev = word.substr(0, i) + word.substr(i + 1);
}

// erase
string getEvery(string s, int index){
    return s.erase(index, 1);
}
for (int i = 0; i < word.size(); i++) {
    string prev = getEvery(word, i);
}
  • 存储26个字符
    • 用vector存储比用unordered_map效率高，开销小
1
2
vector<int> mp(26);
unordered_map<char, int> mp;
  • 直接操作字符串各位效率更高
1
2
3
4
5
6
7
8
9
10
11
12
// s :  hh:mm  24小时时间格式，返回分钟数
int toInt(string& s){
    string sh = s.substr(0, 2);
    string sm = s.substr(3, 2);
    int h = stoi(sh);
    int m = stoi(sm);
    return h*60 + m;
}
// 下面写法效率更高
int toInt(string& t){
    return (int(t[0] - '0') * 10 + int(t[1] - '0')) * 60 + int(t[3] - '0') * 10 + int(t[4] - '0');
}

函数

  • isalnum函数用于判断字符是否为字母（a-z和A-Z）或数字（0-9）
  • reverse
  • 字符串转数字：stoi、atoi 负数也可以转换 前缀0会剔除
  • 数字转字符串：to_string
  • unique + erase 数组去重： c++ unique函数
  • upper_bound(起始迭代器，结束迭代器，比较值a) ：返回严格大于a的元素的迭代器
  • lower_bound : 指向首个不小于 key 的元素的迭代器。若找不到这种元素，则返回尾后迭代器
  • iota() 升序填充值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include<vector>
using namespace std;

int main() {	
	
	vector<int>number(10);

	iota(number.begin(), number.end(), 66);
	for (int i = 0; i < 10; i++) {
		cout << number[i] << " ";		//输出：66 67 68 69 70 71 72 73 74 75
	}

	system("pause");
	return 0;
}
  • accumulate
    • 类似js中reduce
  • memset
    • void *memset(void *s, int c, size_t n);
      • s指向要填充的内存块。
      • c是要被设置的值。
      • n是要被设置该值的字符数。
      • 返回类型是一个指向存储区s的指针。
  • reverse
  • 复杂度:恰好交换 (last - first)/2 次
1
2
int a[] = {4, 5, 6, 7};
std::reverse(std::begin(a), std::end(a));
  • find
1
2
3
std::vector<int> v{0, 1, 2, 3, 4};
 
auto result1 = std::find(std::begin(v), std::end(v), n1);
  • sort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <algorithm>
std::sort(s.begin(), s.end(), std::greater<int>());// 按降序，  默认是升序

// 自定义比较函数
bool compare(vector<int>& a, vector<int>& b){
  if(a[0] != b[0]){
    return a[0] < b[0]; // 起始点小的在前
  }else{
    return a[1] < b[1]; // 起始点相同的情况下，终止点小的在前
  }
}
vector<vector<int>>& intervals;// 存储的是顶点对  [[1,2],[2,3],[3,4],[1,3]]
sort(intervals.begin(), intervals.end(), compare);

// lambda写法
sort(intervals.begin(), intervals.end(), [](vector<int>& a, vector<int>& b){
  if(a[0] != b[0]){
    return a[0] < b[0]; // 起始点小的在前
  }else{
    return a[1] < b[1]; // 起始点相同的情况下，终止点小的在前
  }
});
  • C++中的__builtin_popcount()

https://blog.csdn.net/weixin_44915226/article/details/105367005

1
2
3
4
该函数是C++自带的库函数，内部实现是用查表实现的。
作用：统计数字在二进制下“1”的个数。
int a = 2   
int num = __builtin_popcount(a)  // num = 1   2的二进制是10
  • tie()
    • 解包，类似js中的解构

https://blog.csdn.net/lllzzzhhh2589/article/details/121584299

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
struct S {
    int n;
    std::string s;
    float d;
    bool operator<(const S& rhs) const {
        // 比较 n 与 rhs.n,
        // 而后为 s 与 rhs.s,
        // 而后为 d 与 rhs.d
        return std::tie(n, s, d) < std::tie(rhs.n, rhs.s, rhs.d);
    }
};

S value{42, "Test", 3.14};

int i;
double d;
string s;

tie(i, d, s) = t3;

cout << i << " " << d << " " << s << endl;
//打印： 42 3.14 Test
  • 向上向下四舍五入取整（以下只针对浮点数的运算）
1
2
3
4
5
6
// 向上  
ceil()
// 向下
floor()
// 四舍五入
round()
  • 整数向上取整
1
2
3
4
5
6
// 1
int curh = p%mode == 0 ? 0 : 1;
curh += (p/mode);

// 2
int curh = (p + mode-1)/mode;

常用

STL

stack、vector、list、queue常用方法

stack

  • top

  • push

  • pop

priority_queue

  • top

  • push

  • pop

queue

  • front
  • back
  • push
  • pop

vector

deque

  • front
  • back
  • push_front
  • pop_front
  • push_back
  • pop_back
  • erase
  • shrink_to_fit

list

  • front
  • back
  • push_front
  • pop_front
  • push_back
  • pop_back
  • erase

priority_queue

  • 默认是最大堆
  • 改为最小堆
1
priority_queue<int, vector<int>, greater<int>>
  • 自定义比较函数
1
2
3
4
5
6
7
8
9
10
11
12
13
// 个位数大的在前
bool myCom(int a, int b){
  return a%10 < b%10;
}

priority_queue<int, vector<int>, decltype(myCom)> pq(myCom);

// 转为最小堆
auto cmp = [](ListNode* l1, ListNode* l2){
  return l1->val > l2->val;
};

priority_queue<ListNode*, vector<ListNode*>, decltype(cmp)> pq(cmp); // decltype 用于数据类型的推导

二分查找

lower_bound 返回指向首个不小于给定键的元素的迭代器 (公开成员函数)
upper_bound 返回指向首个大于给定键的元素的迭代器

注意点

容器为空的情况下可以调用 mp.count(key)

容器为空的情况下查找返回的迭代器为 mp.end() , 而容器为空的情况下mp.begin() == mp.end()

1
2
unordered_map<vector<int>, int> mp;  // 报错
map<vector<int>, int> mp; // 正确

输入输出

数据对
  • 没有对数，没有结束标志
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
输入包括两个正整数a,b(1 <= a, b <= 1000),输入数据包括多组。

输入例子：
1 5
10 20
输出例子：
6
30

int main() {
    int a, b;
    while (cin >> a >> b) { // 注意 while 处理多个 case
        cout << a + b << endl;
    }
}
  • 有结束标志
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
输入包括两个正整数a,b(1 <= a, b <= 10^9),输入数据有多组, 如果输入为0 0则结束输入
输入例子：
1 5
10 20
0 0  
输出例子：
6
30
    
int main() {
    int a, b;
    while (cin >> a >> b) { // 注意 while 处理多个 case
        if(a == 0 && b == 0) break;
        cout << a + b << endl;
    }
}
多行数据
  • 有结束标志
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
输入数据包括多组。
每组数据一行,每行的第一个整数为整数的个数n(1 <= n <= 100), n为0的时候结束输入。
接下来n个正整数,即需要求和的每个正整数。

输入例子：
4 1 2 3 4
5 1 2 3 4 5
0
输出例子：
10
15

int main() {
    while (true) {
        int n;
        cin >> n;
        if (n == 0) {
            break;
        }
        vector<int> nums(n);
        int sum = 0;
        for (int i = 0; i < n; i++) {
            cin >> nums[i];
            sum += nums[i];
        }
        cout << sum << endl;
    }
    return 0;
}
  • 有行数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
输入的第一行包括一个正整数t(1 <= t <= 100), 表示数据组数。
接下来t行, 每行一组数据。
每行的第一个整数为整数的个数n(1 <= n <= 100)。
接下来n个正整数, 即需要求和的每个正整数。

输入例子：
2
4 1 2 3 4
5 1 2 3 4 5
输出例子：
10
15

int main() {
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        vector<int> nums(n);
        int sum = 0;
        for (int i = 0; i < n; i++) {
            cin >> nums[i];
            sum += nums[i];
        }
        cout << sum << endl;
    }
    return 0;
}
  • 没有行数，没有结束标志
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
输入数据有多组, 每行表示一组输入数据。
每行的第一个整数为整数的个数n(1 <= n <= 100)。
接下来n个正整数, 即需要求和的每个正整数。

输入例子：
4 1 2 3 4
5 1 2 3 4 5
输出例子：
10
15

int main() {
    string line;
    while (getline(cin, line)) {
        stringstream ss(line);
        int n ;
        ss >> n;
        vector<int> vec(n);
        int sum = 0;
        for (int i = 0; i < n; ++i) {
            ss >> vec[i];
            sum += vec[i];
        }
        cout << sum << endl;
    }
    return 0;
}
  • 没有每行数据个数，没有行数，没有结束标志
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
输入数据有多组, 每行表示一组输入数据。

每行不定有n个整数，空格隔开。(1 <= n <= 100)。
    
输入例子：
1 2 3
4 5
0 0 0 0 0
输出例子：
6
9
0
    
int main() {
    string line;
    while (getline(cin, line)) {
        istringstream iss(line);
        int num;
        int sum = 0;
        vector<int> vec;
        while (iss >> num) {
            vec.push_back(num);
            sum += num;
        }
        cout << sum << endl;
        // for(int i = 0; i < vec.size(); ++i){
        //     cout<<vec[i]<<" ";
        // }
        // cout<<endl;
 
    }
    return 0;
}
多个字符串
  • 给定个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
输入有两行，第一行n

第二行是n个字符串，字符串之间用空格隔开

输入例子：
5
c d a bb e
输出例子：
a bb c d e

int main(){
  int n;
  cin>>n;
  cin.ignore();
  string line;
  getline(cin,line);
  stringstream ss(line);
  vector<string> vec(n);
  for(int i = 0; i < n; ++i){
    ss>>vec[i];
  }
  sort(vec.begin(), vec.end());
  for(int i = 0 ; i < n; ++i){
    if(i != n-1)
      cout << vec[i]<< " ";
    else
      cout<< vec[i]<<endl;
  }
   
}
  • 多行字符串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
多个测试用例，每个测试用例一行。

每行通过空格隔开，有n个字符，n＜100

输入例子：
a c bb
f dddd
nowcoder
输出例子：
a bb c
dddd f
nowcoder

int main(){
  string line;
  while (getline(cin, line))
  {
    istringstream iss(line);
    string s;
    vector<string> vec;
    while (iss>>s)
    {
      vec.push_back(s);
    }
    sort(vec.begin(), vec.end());
    for(int i = 0; i<vec.size(); ++i){
      if(i!=vec.size() -1)
        cout<<vec[i]<<" ";
      else
        cout<<vec[i]<<endl;
    }
     
  }
  return 0;
   
}
  • 多行字符串，每个字符串用逗号隔开
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
多个测试用例，每个测试用例一行。
每行通过,隔开，有n个字符，n＜100

输入例子：
a,c,bb
f,dddd
nowcoder
输出例子：
a,bb,c
dddd,f
nowcoder


int main() {
    string line;
    while (getline(cin, line)) {
        istringstream iss(line);
        string s;
        vector<string> vec;
        while (getline(iss, s, ',')) {
            vec.push_back(s);
        }
        sort(vec.begin(), vec.end());
        for (int i = 0 ; i < vec.size(); ++i) {
            if (i != vec.size() - 1)
                cout << vec[i] << ",";
            else
                cout << vec[i] << endl;
        }
 
    }
    return 0;
}

字符串

ASCII码一览表

1
2
INT_MAX = 2^31-1;
INT_MIN = -2^31

字符串转int

atoi()和stoi()

  • atoi()和stoi()函数都是只转换字符串的数字部分，如果遇到其它字符的话则停止转换
  • 只返回有效数字 0123返回123

atoi()和stoi()的区别

  • 相同点

    • 都是C++的字符处理函数，把数字字符串转换成int输出

    • 头文件都是#include<cstring>

  • 不同点

  • <1>参数类型不同

    • atoi()的参数是 const char* ,因此对于一个字符串str我们必须调用 c_str()的方法把这个string转换成 const char*类型。

    • stoi()的参数是const string&,不需要转化为 const char*

  • <2>范围检查

    • atoi()不会做范围检查，如果超出范围的话，超出上界，则输出上界，超出下界，则输出下界；
    • stoi()会做范围检查，默认范围是在int的范围内的，如果超出范围的话则会吐核超出范围。

img

string转char

c_str()

C++中的 c_str() 函数

1
2
3
4
5
6
7
8
9
10
11
12
13
#include<iostream>
#include<cstring>
using namespace std;

int main() {
	const char *ptr;
	string s = "12345";
    ptr = s.c_str();
    cout << "s改变前ptr为：" << ptr << endl;
    s = "66666";
    cout << "s改变后ptr为：" << ptr << endl;
    return 0;
}

int转string

to_string()

大小写字符转换

tolower/toupper 

1
2
#include<ctype.h>   // c++中使用不用引入头文件
// 只能单个字符转换

判断字符数字

  • isalnum函数用于判断字符是否为字母（a-z和A-Z）或数字（0-9）

isalnum

1
#include<ctype.h> // c++中使用不用引入头文件

string移除最后一个元素

1
2
string s = "string!";
s.pop_back(); // c++11 新语法

string追加char

1
2
3
4
5
6
7
string s = "abc";
char c = 'd';
// 方式1
s += c;
cout<<s<<endl;
// 方式2
s.push_back(c);

位运算

https://blog.csdn.net/m0_64183293/article/details/122519405

GCC自带的一些builtin内建函数 ：https://blog.csdn.net/tjcwt2011/article/details/118154919

  • C++中的__builtin_popcount()

https://blog.csdn.net/weixin_44915226/article/details/105367005

1
2
该函数是C++自带的库函数，内部实现是用查表实现的。
作用：统计数字在二进制下“1”的个数。
  • __builtin_ctz
    • 这个函数作用是返回输入数二进制表示从最低位开始(右起)的连续的0的个数；如果传入0则行为未定义

二进制1个数

三种求二进制1个数的办法

1
2
3
1 __builtin_popcount
2 x >> 1  x & 1   右移，末尾和1与
3 x = x & (x-1)

位与位异或位或

https://blog.csdn.net/m0_37782602/article/details/122863949

1
2
3
位与 &  0&0=0; 0&1=0; 1&0=0; 1&1=1;
位异或 ^ 0^0=0； 0^1=1； 1^0=1； 1^1=0；
位或 |  0|0=0； 0|1=1； 1|0=1； 1|1=1；
1
Brian Kernighan 算法的原理是：对于任意整数x, 令 x = x & (x-1) 该运算将 x 的二进制表示的最后一个 1 变成 0

数值

1
1e9+7 // 10^9+7  一个比较大的质数

取绝对值

abs()

使用最大最小值

1
2
3
<limits.h>
LONG_MIN
L

保留小数点后n位**

https://zhidao.baidu.com/question/1431242996370114299.html

  • setprecision(n) : 表示保留n位，整体保留的位数
  • fixed： 表示以小数点后开始记保留的位数
1
2
3
4
#include <iomanip>
double cur = 4.6666667
cout<<setprecision(4)<<cur<<endl; // 4.667
cout<<fixed<<setprecision(4)<<cur<<endl; // 4.6667